LA TERRE

AURORE. — Imaginez une grosse boule suspendue en l'air par un fil ; et sur cette boule un moucheron. S'il prend fantaisie au moucheron d'en parcourir la surface, n'est-il pas vrai qu'il pourra aller et venir sur la boule, en dessus, en dessous, par côté, sans jamais rencontrer d'obstacle, sans jamais voir se dresser une barrière qui lui ferme le passage ? N'est-il pas également vrai que, s'il chemine toujours dans la même direction, le moucheron finira par faire le tour de la boule et par revenir à son point de départ ?

AUGUSTINE. — Rien n'est plus clair.

AURORE. — Ainsi faisons-nous nous-mêmes à la surface de la Terre, plus chétifs par rapport à l'immensité du globe qui nous porte que le moindre moucheron par rapport a la boule la plus considérable que votre imagination puisse se figurer. Sans rencontrer nulle part de barrières, nous allons et venons en mille sens différents, nous accomplissons les voyages les plus lointains, nous faisons même le tour de la Terre et revenons au point de départ.

La Terre est donc ronde : c'est une boule immense qui nage dans les espaces du ciel. Quant à la voûte bleue qui s'arrondit au-dessus de nous, vous savez que c'est une simple apparence produite par l'atmosphère, c'est-à-dire par l'épaisse couche d'air qui de partout nous enveloppe.

AUGUSTINE. — La boule sur laquelle voyage le moucheron que vous supposez est suspendue à un fil. A quelle chaîne est donc suspendue la grosse boule de la Terre ?

AURORE. — La Terre n'est pas suspendue au firmament par quelque chaîne céleste ; elle n'est pas davantage appuyée sur un support, comme un globe géographique sur son pied. D'après un conte de l'Inde, la boule du monde est portée sur quatre colonnes de bronze.

CLAIRE. — Et ces quatre colonnes, sur quoi reposent-elles à leur tour ?

AURORE. — Elles reposent sur quatre éléphants blancs.

CLAIRE. — Et les éléphants blancs ?

AURORE. — Ils s'appuient sur quatre monstrueuses tortues.

CLAIRE. — Et les tortues ?

AURORE. Eh bien, elles nagent sur un océan de lait.

CLAIRE. — Et l'océan de lait ?

AURORE. — Le conte n'en dit rien, et il a raison de garder le silence. Il aurait même mieux fait de ne pas imaginer, pour soutenir la Terre, ces divers supports se servant d'appui l'un à l'autre.

MARIE. — Si l'on imagine un support pour cette mer de lait, il n'en faudra pas moins chercher après ce qui soutient ce support ; et toujours ainsi sans jamais finir.

AURORE. — Marie voit fort bien la difficulté. Supposer un piédestal à la Terre, puis un second pour soutenir le premier, ensuite un troisième, un quatrième, un millième, si l'on veut, c'est éloigner la question sans y répondre car enfin, après avoir mis l'un sur l'autre tous les supports imaginables, il faudra se demander sur quoi repose le dernier.

AUGUSTINE. — Je dirai qu'il repose sur la voûte du ciel.

AURORE. — Vous oubliez donc que cette voûte n'a aucune réalité, qu'elle est simplement une trompeuse apparence résultant de l'atmosphère.

AUGUSTINE. — Ah ! L'étourdie ! Je n'y songeais plus.

AURORE. — Sachez enfin que des milliers de voyageurs ont parcouru la Terre en tous sens, et qu'ils n'ont vu nulle part ni chaîne de suspension, ni piédestal quelconque. On ne voit partout que ce que l'on voit ici. La Terre est, par conséquent, isolée dans l'espace ; elle nage dans l'étendue sans aucun appui, comme nagent la Lune et le Soleil.

CLAIRE. — Mais alors pourquoi ne tombe-t-elle pas ?

AURORE. — Et sur quoi voulez-vous qu'elle tombe ? Tomber, ma petite amie, c'est se précipiter à terre, comme le fait une pierre qui, soulevée dans la main, est ensuite abandonnée à elle-même. Comment voulez-vous que la grosse boule se précipite à terre, elle qui est toute la terre ? Est-il possible qu'une chose se précipite vers cette chose elle-même.

CLAIRE. — Certes, non.

AURORE. — Eh bien, alors ! D'ailleurs, figurez-vous ceci : tout étant pareil autour de la boule du monde, il n'y a réellement ni haut ni bas. Nous appellerons le haut, si vous voulez, le côté de l'espace qui est au-dessus de nos têtes, le côté du ciel ; mais songez qu'un ciel pareil se trouve aussi à l'extrémité opposée de la boule, exactement comme nous le voyons ici, et que cela se reproduit partout. Le haut, le ciel, est par conséquent dans toutes les directions à la fois. Vous ne vous êtes jamais demandé pourquoi la Terre ne se précipite pas dans l'étendue qui est au-dessus de nos têtes; ne vous demandez pas davantage pourquoi elle ne se précipite pas dans l'étendue opposée, car, dans les deux cas, c'est exactement la même chose : c'est s'élever et non tomber.

CLAIRE. — Au fait, s'élancer vers le ciel, c'est bien s'élever. La Terre ne peut donc tomber. Après ?

AURORE. — J'ai dit que la Terre a la forme d'une immense boule. Je le prouve. Lorsque, pour arriver à la ville où il se rend, un voyageur traverse une plaine régulière où rien n'entrave la portée de la vue, à une certaine distance les points les plus élevés de la ville, les sommets des tours et des cloches, se montrent seuls à ses regards. A une distance moindre, les flèches des clochers deviennent en entier visibles, puis les toits des habitations, et enfin les habitations elles-mêmes ; de sorte que la vue embrasse un plus grand nombre d'objets, en commençant par les plus élevés et en finissant par les plus bas, à mesure que l'éloignement diminue. La courbure du terrain en est cause.

Aurore prit de la craie et traça au tableau noir la figure que voici ; puis elle reprit :

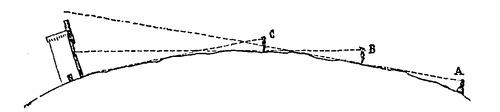
Figure 1

Pour un observateur placé en A, la tour est complètement invisible, parce que la courbure du sol met obstacle à la vue. Pour l'observateur en B, la moitié supérieure de la tour est visible, mais la moitié inférieure est encore cachée. Enfin, quand l'observateur est en C, il peut voir la tour en entier.

Ce n'est pas ainsi que les choses se passeraient si la terre était plate. A toute distance, une tour serait visible en entier. De loin, sans doute, on la verrait avec moins de netteté que de près, à cause de la distance, mais enfin on la verrait tant bien que mal du sommet à la base.

Ici nouveau dessin d'Aurore, représentant deux spectateurs A et B (fig. 2), qui, placés à des distances fort différentes, voient cependant la tour du sommet à la base sur un terrain plat. Aurore reprit :

Figure 2

Sur la terre ferme, il est rare de trouver des terrains qui, par leur étendue et leur régularité, se prêtent à l'observation dont je viens de vous parler. Presque toujours des collines, des plis du sol, des rideaux de verdure arrêtent le regard et empêchent de voir apparaître peu à peu, du sommet à la base, la tour ou le clocher dont on se rapproche. Sur mer, aucun obstacle n'arrête la vue, si ce n'est la courbure des eaux, qui possèdent avec une régularité parfaite la configuration générale de la Terre. C'est donc là surtout qu'il est facile de constater les apparences produites par la forme arrondie.

Figure 3

Lorsqu'une barque venant de la pleine mer se rapproche des côtes, les premiers points du rivage visibles pour les gens qui la montent sont les points les plus élevés, comme les cimes des montagnes. Plus tard apparaissent les sommets des hautes tours ; plus tard encore, le bord du rivage lui-même. Pareillement, un observateur qui, du rivage, assiste à l'arrivée d'un navire, commence par apercevoir la pointe des mâts, puis les voiles les plus hautes, puis encore, les voiles basses, et enfin la coque du navire.

Si le navire s'éloignait du rivage, on le verrait graduellement disparaître et plonger en apparence sous les eaux dans un ordre inverse, c'est-à-dire que la coque se déroberait la première aux regards, puis les voiles basses, les voiles hautes et enfin la cime du grand mat, qui disparaitrait la dernière.

AURORE. — La Terre a quarante millions de mètres de tour, ou bien dix milles lieues, car une lieue mesure quatre mille mètres.

CLAIRE. — Pour faire à pied ces dix mille lieues, quel temps faudrait-il ?

AURORE. — Un voyageur capable, par impossible, de reprendre chaque matin sa marche en avant, à raison de dix lieues par jour, mettrait de trois à quatre ans pour faire à pied le tour de la boule terrestre, en supposant que la terre ferme ne fût pas interrompue par des mers. Mais où sont les jarrets qui résisteraient quatre ans de suite à de telles fatigues, lorsqu'un trajet de dix lieues épuise le plus souvent nos forces, et nous met dans l'impossibilité de recommencer le lendemain !

AUGUSTINE. — Je vois bien que le petit garçon dont vous nous avez raconté le projet d'aller au bout du monde n'avait, pour un pareil voyage, ni d'assez bonnes jambes, ni d'assez abondantes provisions, bien qu'il eût mis dans son panier deux pommes, six noix et une tartine de beurre. Le plus grand trajet à pied que j'aie fait est celui des montagnes voisines, avec mon frère. Combien cela fait-il de lieues ?

AURORE. — Quatre environ, deux pour aller et deux pour revenir.

AUGUSTINE — Rien que quatre lieues ! J'étais pourtant bien fatiguée. À la fin, je ne pouvais plus mettre une jambe devant l'autre. Il me faudrait alors, pour faire le tour du monde en marchant chaque jour autant que me le permettent mes forces ?...

AURORE. — Il vous faudrait de huit à dix ans.

AUGUSTINE. — Au retour du voyage, je serais une grande demoiselle. Elle est donc bien grosse, la boule du monde ?

AURORE. — Oui, ma fille, très-grosse. Un autre exemple va vous aider à le comprendre.

Représentons le globe terrestre par une boule plus grande que hauteur d'homme, puis, dans une juste proportion, représentons en relief, à sa surface, quelques-unes des principales montagnes. Le mont le plus élevé de la Terre est le Gaurisankar, qui fait partie de la chaîne de l'Himalaya, vers le centre de l'Asie. Il dresse ses pics à 8,840 mètres de hauteur. Rarement les nuages sont assez élevés pour en couronner la cime, et sa base recouvre l'étendue d'un empire. Eh bien, élevons le géant sur notre grosse boule figurant la Terre ; savez-vous ce qu'il faudra pour le représenter ? Il faudra un tout petit grain de sable qui se perdrait entre vos doigts, un grain de sable d'un millimètre et un tiers de relief ! La gigantesque montagne qui nous accable de son immensité n'est plus rien quand on la compare à la Terre. La plus grande montagne de l'Europe, le mont Blanc, dont la hauteur est de 4,810 mètres, serait figurée par un grain de sable moitié moindre.

MARIE. — Quand vous parliez de la rondeur de la terre, je songeais aux montagnes énormes, aux vallées profondes, et je me demandais comment, avec toutes ses grandes irrégularités, la Terre cependant petit être qualifiée de ronde. Je vois maintenant que ces irrégularités ne sont rien par rapport à l'immensité de la boule terrestre.

AURORE. — Une orange est ronde, malgré les rugosités de son écorce. Il en est ainsi de la Terre : elle est ronde, malgré les rugosités de son écorce, moindres, toutes proportions gardées, que celles de l'orange. C'est une énorme boule semée de grains de poussière et de sable proportionnés à sa grosseur, et qui sont les montagnes.

AUGUSTINE. — Quelle grosse boule !

AURORE. — Mesurer le tour de la Terre n'est pas chose facile, vous vous en doutez bien; et cependant on a fait mieux : on a pesé la boule immense, comme s'il était possible de la mettre dans le bassin d'une balance avec des kilogrammes pour contre-poids. La science, mes chères enfants, a des ressources où se montre, dans toute sa grandeur, la puissance de l'esprit humain. On a pesé la colossale boule. On ne s'est pas servi de la balance, mais de la puissance de la pensée, que Dieu a mise en nous pour déchiffrer à sa gloire la sublime énigme de l'univers ; de la force de la raison, pour qui n'est pas trop lourd le fardeau de la Terre. Ce fardeau est exprimé par le chiffre 6, suivi de vingt et un zéros, ou bien par 6 sextillions de kilogrammes.

CLAIRE. — Ce nombre ne m dit rien : il est trop grand.

AURORE. — C'est l'inconvénient de tous les grands nombres. Prenons alors un détour. Supposons la Terre déposée sur un char et traînée sur une surface analogue à celle de nos routes. Pour un tel fardeau, quel doit être l'attelage ? — Mettons de front un million de vigoureux chevaux ; et, par devant cette rangée, une seconde encore d'un million ; puis une troisième, toujours d'un million; et continuons ainsi jusqu'à mille rangées. Nous aurons de la sorte un attelage de mille millions de chevaux, plus que n'en pourraient nourrir tous les pâturages du monde. Et maintenant, allez, donnez du fouet ! — Rien ne bougerait, mes enfants ; la force serait insuffisante. Pour ébranler la gigantesque masse, il faudrait les efforts réunis de cent millions d'attelages pareils !

CLAIRE. — Je ne comprends pas davantage.

AURORE. — Ni moi non plus, tant c'est énorme.

CLAIRE. — Oui, énorme, ma tante.

MARIE. — Tellement, que l'esprit s'y perd. C'est ce que je désirais vous faire avouer.

AURORE. — C'est ce que je désirais vous faire avouer.

source : Jean-Henri Fabre, Aurore, 1874